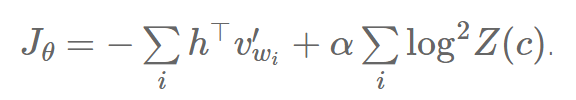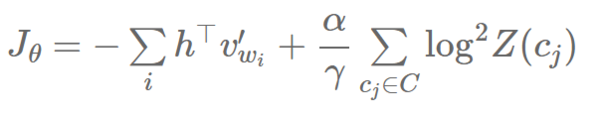如果我们可以限制我们的模型，使得它可以让 Z(c)=1 或 logZ(c)=0，那么我们可以避免计算标准化项 Z(c)。Devlin 等人（2014 年）因此提出给损失函数加上一个平方错误惩罚项，来鼓励模型把 Z(c) 保持着尽量接近 0：

这可以写成：

　　其中 α 允许我们去做模型准确度和平均数自标准化的取舍。我们大体就可以保证 Z(c) 将和我们希望的一样非常接近于 1。在它们的 MT 系统的解码时间内，Devlin 等人（2014 年）接着设置 softmax 的分母为 1，而且仅仅使用分母和它们的惩罚项来计算 P(w|c) ：

他们称自标准化加速了大概 15 倍，而相比于常规的非自标准化的神经语言模型，在 BLEU 分数上只有少量的退步。

低频的标准化方法

Andreas 和 Klein [11] 提出仅仅标准化一部分训练样本已经足够，且仍能获得和自标准化一样的行为。他们由此提出低频的标准化（Infrequent Normalisation，或 IN），仅仅在惩罚项中取小部分样本，来形成一个基于样本的方法。

让我们先来把之前的损失函数 Jθ 分解成两个独立的和：

我们现在在训练数据中，通过仅仅计算一个词的子集 C（它包含词 wj）来在第二项中取小部分样本，从而从上下文 cj 采样（因为 Z(c) 仅依赖于上下文 c）：

其中，γ 控制着子集 C 的大小。Andreas 和 Klein（2015 年）提出 IF 综合了 NCE 和自标准化的优点，因为它不用给所有的训练样本计算标准化项（NCE 完全不用计算），但是又像自标准化一样允许去做模型准确度和平均数自标准化的取舍。他们观察到当它只用从十分之一的样本中采样时，它能够加速 10 倍，而没有明显的模型表现损失。

其它方法

至此，我们已经集中讲解了近似或者完全避免 softmax 分母 Z(c) 的计算的方法，因为它就是计算中最昂贵的一项。我们因此不去特别留意

　　，

即倒数第二层 h 和输出词嵌入层 v′w 的点积。Vijayanarasimhan 等人 [12 ] 提出用快速的位置敏感哈希（locality-sensitive hashing）来近似

然而，尽管这个方法在测试阶段可以加速模型，但是在训练阶段，这个加速实际上会消失，因为词嵌入必须重新标号，且批（batch）的数量会增加。

选择哪个方法呢？

　　看完了最流行的基于 softmax 的和机遇采样的方法，我们展示了对于经典的 softmax 有很多替代品，而且几乎它们所有都在速度上有重要提升，它们大多数也略有模型表现上的不足。所以，这自然引到了一个问题，就是对于某一个特定的任务，哪个方法是最好的方法。