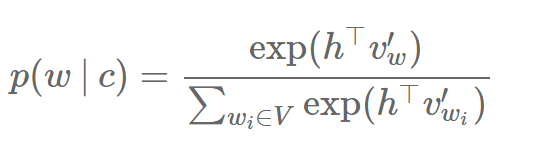基于Softmax的方法

多层次Softmax

微分Softmax

CNN-Softmax

基于采样（Sampling）的方法

重要性采样

具有适应的重要性采样

目标采样

噪音对比估计

负采样

自标准化

低频的标准化

其他方法

选择哪一种方法？

结论

这篇博文是我们词嵌入及其表示系列的第二篇。在上一篇博文里，我们提供了词嵌入模型的概述，并介绍了 Bengio 等人在2003年提出的经典神经语言学习模型、Collobert 和 CWeston 在2008年提出的 C&W 模型，以及Mikolov 在2013年提出的 word2vec 模型。我们发现，设计更好的词嵌入模型的最大挑战，就是如何降低softmax 层的计算复杂度。而且，这也是机器翻译（MT）（Jean等人[10 ]）和语言建模（Jozefowicz等人[6 ]）的共通之处。

在这篇博文里，我们将要重点介绍过去几年的研究中 softmax 层的不同近似方法，它们其中的一些被运用在语言建模和机器学习。在下一篇博文里，我们才会介绍别的超参数。

为了统一以及便于比较，让我们简单重新介绍一下上一篇博文的重点：我们假设训练集是一串包括 T 个训练词的字符序列 w1,w2,w3,?,wT ，每一个词来源于大小为 |V| 的词汇库 V。模型大体上考虑n个词的上下文 c。我们将每一个词和一个 d 维度的输入向量（也就是表示层的词嵌入）vw 以及输出向量 v′w（在softmax层的权重矩阵的对于词的表示）联系在一起。最终，我们相对于我们的模型参数 θ 来优化目标函数 Jθ。

我们一起来回顾一下，softmax 层对于一个词 w 在上下文 c 出现的概率的计算公式如下：

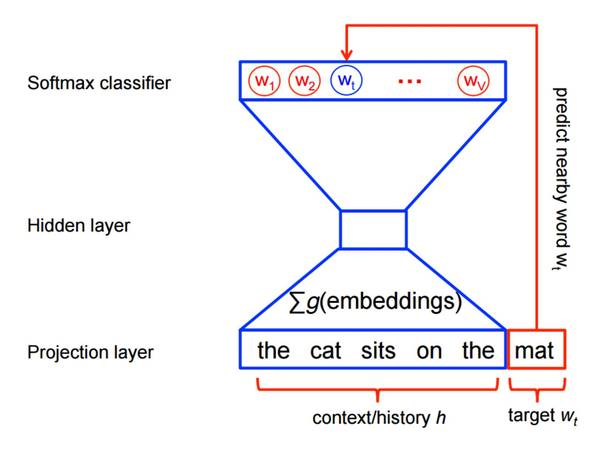
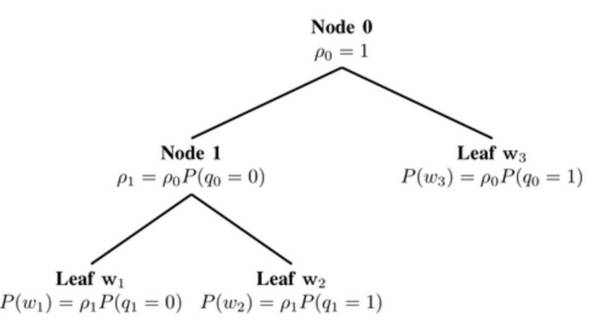
　　其中，h 是倒数第二层的输出向量。注意到和之前提到的一样，我们用c来表示上下文，并且为了简洁，舍弃目标词 wt 的索引 t。计算softmax的复杂度很高，因为计算 h 和 V 里每个词 wi 的输出向量的内积需要通过一部分的分母的求和来获得，从而得到标准化后目标词 w 在上下文 c 的概率。

接下来我们将会讨论近似 softmax 所采用的不同方法。这些方法可以分成两类：一类是基于 softmax 的方法，另一类则是基于采样的方法。基于 softmax 的方法保证 softmax 层的完好无损，但是修改了它的结构来提升它的效率。基于采样的方法则是完全去掉 softmax 层，优化其它目标函数来近似 softmax。

基于 softmax 的方法

多层次的 softmax 方法

多层次的softmax（H－Softmax）是 Morin 和 Bengio[3]受到二叉树启发的方法。根本上来说，H-softmax 用词语作为叶子的多层结构来替代原 softmax 层的一层，如图1所示。

多层次的softmax（H－Softmax）是 Morin 和 Bengio[3]受到二叉树启发的方法。根本上来说，H-softmax 用词语作为叶子的多层结构来替代原 softmax 层的一层，如图1所示。

这让我们把对一个词出现概率的计算分解成一连串的概率计算，我们将无需对所有词作昂贵的标准化。用 H-Softmax 来替代单一的 softmax 层可以把预测词的任务带来至少50倍的速度提升，因此适用于要求低延迟的任务，比如 Google 的新通讯软件 Allo 的实时沟通功能。

图 1：多层词的 softmax

我们可以把常规的 softmax 想成是只有一层深度的树，每个 V 中的词都是一个叶子节点。计算一个词的 softmax的概率则需要标准化所有 |V| 个叶子的概率。反之，如果我们把 softmax 当成一个每个词都是叶子的二叉树，我们只需要从叶子节点开始沿着树的路径走到那个词，而无序考虑其它的词。

因为一个平衡的二叉树的深度为 log2(|V|)，我们只需要通过计算最多 log2(|V|) 个节点来取得一个词最终的概率。注意到这个概率都已经经过了标准化，因为二叉树中所有叶子节点的概率之和为1，所以形成了一个概率分布。想要粗略地验证它，我们可以推理一个树的根节点（图1中的节点0），它的所有分支必须相加为1。对于每个接下来的节点，概率质量分解给它的分支，直到最终到达叶子节点，也就是词。因为这其中没有损失概率，而且所有词都是叶子，所有词的概率的总和必须为1，所以分层次的 softmax 定义了在 V 上所有词的一个标准化的概率分布。