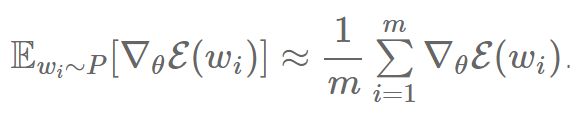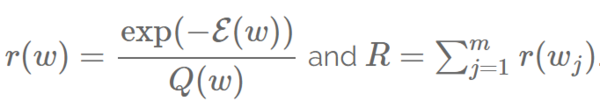我们现在可以用蒙特卡洛方法去近似任何概率分布的期待值 E，也就是所有概率分布的随机样本的平均值。如果我们知道网络的分布，即 P(w)，我们就可以从中采样 m 个词 w1,?,wm ，然后近似得到如上的期望：

　　然而，为了从概率分布 P 中采样，我们需要计算 P，但这其实是我们最开始想要避免的。于是，我们找到另一个概率分布 Q，我们称之为建议分布（proposal distribution）。Q 应该便于从中采样，而且可以用来作为蒙特卡洛抽样法的基础。我们偏向于选取和 P 相近的概率作为 Q，因为我们希望得到的近似期望能够尽量准确。在语言建模中一个非常直接的选择就是用一元文法分布（unigram distribution）作为 Q 的训练集。

这也就是经典的重要性抽样方法（Importance Sampling，英文缩写 IS)：它使用蒙特卡洛抽样，通过一个提议分布Q来近似一个目标概率分布 P。然而，这仍然需要给每个采样的词 w 计算 P(w)。为了避免这个，Bengio 和 Senécal (2003年) 用Liu [16]中提出的有偏估计量（biased estimator）。这个预测函数可以在 P(w) 当成乘积计算时使用，这正是我们要处理的情况，因为每个除法都可以转化成乘法。

从根本上来说，我们不必花大代价计算 Pwi 并得到梯度 ?θE(wi) 的权重，我们只需要利用提议分布Q来得到权重的一个因子。对于一个有偏见的 IS，这个因子就是

　　其中

且

　　请注意，我们用 r 和 Q 而非 Bengio 和 Senécal (2003年, 2008年) 论文中的 w 和 W 来避免重名。因为我们可以发现，我们仍然计算 softmax 的分母，但是用提议分布 Q 来替换分母的标准化。因此，我们的用以近似期望的有偏差的预测函数如下：

请注意，我们用越少的样本，我们的预测就会越差。另外，我们需要在训练阶段调整我们的样本数量，因为如果样本数量太小，在训练阶段，网络的分布 P 可能和一元分布 Q 分岔，导致整个模型无法收敛。因此，Bengio 和 Senécal 为了防止可能的分岔采用了一个计算有效样本大小的方法。最后，研究者们声称这个方法相对于传统的softmax能够加速19倍。

自适应性重要性采样方法

　　Bengio 和 Senécal (2008年) 注意到对于重要性采样方法，替换掉越多复杂的概率分布，比如二元（bigram）和三元（trigram）分布，那么接下来在训练阶段，将对于从模型的真实分布 P 来对一元分布 Q 的分岔的对抗将无效，因为n元（n-gram）分布看起来和训练好的神经语言模型的分布挺不一样。作为替代模型，他们提出了一个用在训练阶段调整适应过的 n 元分布来更好地跟随目标分布P。最后，他们根据一些混合方程来插值（interpolate）一个二元分布和一个一元分布，而这些混合方程的参数都是他们用不同频率组的 SGD 训练的，训练目标为最小化目标分布 P 和提议分布 Q 的 Kullback-Leibler 差异。在实验中，他们声称训练效果提高了大约100倍。

目标采样方法

Jean 等人（2015年）提出了在机器翻译中运用具有适应性的重要性采样方法。为了让模型更好地适应 GPU 上的并行计算及有限内存，他们将目标单词的数量限制到采样最少必须达到的数量。他们将训练集分区，在每个分区只保留一定数量的单词，形成了总词汇表的一个分集 V′。

这根本上表现了一个独立的提议分布 Qi 可以在训练集的每个分区 i 中运用，这给所有词汇表分集 V′i 内的词赋予同等的概率，而其它的词则概率为0。

噪音对比估计方法

噪音对比估计 （NCE）（Gutmann 和 Hyvärinen） [17] 由 Mnih 和 Teh [18] 作为一个比重要性采样方法（IS）更稳定的采样方法提出，因为我们发现 IS 具有一定风险出现建议分布 Q 和分布 P 分岔的情况，而这就是需要优化的地方。不同于之前的方法，NCE 并没有试图直接预测一个词的概率，而是用一个辅助性的损失函数来同时最大化正确词的概率。