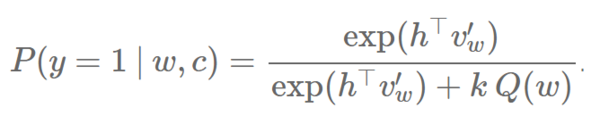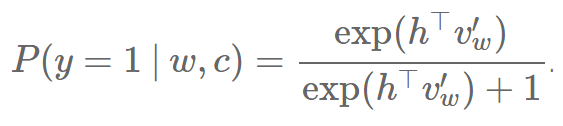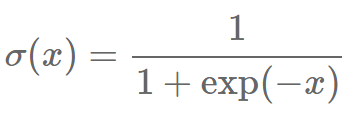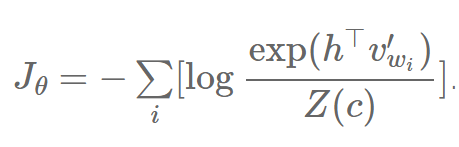一个 NCE 的缺点就是，因为不同的噪音样本来源于对每个训练词 w 的采样，噪音样本和它们的梯度都不能在稠密矩阵中存储，这减少了在 GPU 上使用 NCE 的好处，因为它不能受益于快速稠密矩阵乘法运算。Jozefowicz 等人（2016 年）和 Zoph 等人（2016 年）独立地提出在所有训练词中共享噪音样本，从而 NCE 的梯度可以用稠密矩阵运算来计算，在 GPU 上更加高效。

NCE 和 IS 的相似性

Jozefowicz 等人（2016 年）的研究认为 NCE 和 IS 不仅都是基于采样的方法，同时也高度关联。他们发现 NCE 用一个二元分类的任务，IS 可以类似地用一个代理损失函数（也称上界损失函数，surrogate loss function）表示：IS 并不像 NCE 一样用一个 logistic 损失函数去做二元分类任务，而是优化用一个 softmax 和一个交叉熵损失函数做一个多元分类的任务。他们发现当 IS 做多元分类的任务时，它为语言建模提供了一个更好的选择，因为损失函数带来了数据和噪音样本的共同更新，而不是像 NCE 一样的独立更新。事实上，Jozefowicz 等人（2016 年）用 IS 做语言建模，并在 1B Word Benchmark 数据上却取得了优异表现（就像上文所述）。

负采样方法

Mikolov 等人（2013）发现并推广的目标——负采样（NEG），可以被看成是 NCE 的一个近似。就像我们之前所说的，NCE 可以被证明是在样本数量 k 增大后对 softmax 损失函数的近似。NCE 的简化算法 NEG 避开了这个保证，因为 NEG 的目标就是学习高质量的词表征，而不同于在测试集上获得低困惑度这一个语言建模的目标。

NEG 也用一个 logistic 损失函数来最小化训练集内的词的负对数可能性。让我们回忆一下，NCE 计算给定上下文 c 一个来自实际的训练概率分布 Ptrain 的词 w 的概率，如下：

NCE 和 NEG 的主要差别在于 NEG 只是用简化 NEG 的计算来近似这一个概率。因此，它将最昂贵的项 kQ(w) 设为 1，我们就得到：

　　当 k=|V| 而且 Q 是一个均等分布时，kQ(w)=1 刚好为真。在这个情况下，NEG 等价于 NCE。我们设 kQ(w)=1 而不是其它常数的原因可以从重写这个算式来得到，因为 P(y=1|w,c) 可以变型成 sigmoid 函数

　　如果我们将它插入回之前的 logistic 回归函数中，我们得到：

稍微简化一下，我们得到：

设:

　　最终得到 NEG 损失函数：

　　为了和 Mikolov 等人（2013 年）的标号统一起来，h 必须被 vwI 替换，v′wi 需被 v′wO 替换，以及 vw~ij 需被 v′wi 替换。另外，和 Mikolov 的 NEG 的目标相反，我们 a) 在整个词汇集中优化目标，b) 最小化负对数可能性而非最大正对数可能性（如上文所说），和 c) 已经把

　　的期望替换成它的蒙特卡洛近似。对于更多推导 NEG 的信息，敬请参见 Goldberg 和 Levy 的笔记 [22]。

我们已经看到 NEG 只是在 k=|V| 而且 Q 是一个均等分布时和 NCE 相等价。在其它情况下，NEG 只是和 NCE 近似，也就是说它并没有直接优化正确词的可能性，这是语言建模的关键。虽然 NEG 可能因此对于学习词嵌入非常有用，但是它不能保证渐近一致性（asymptotic consistency），这使得它不适合语言建模。

自标准化方法

　　虽然 Devlin 等人 [23] 提出的自标准化技术（self-normalisation）不是一个基于样本的方法，它为语言模型的自身标准化技术更直观，我们待会儿会介绍。我们之前提到的把 NCE 的损失函数的分母 Z(c) 设为 1，这个函数实质上自标准化了。这是一个有用的性质，因为它允许我们跳过标准化项 Z(c) 的昂贵计算。

请回忆，我们的损失函数 Jθ 最小化我们的训练数据的所有词 wi 的负对数可能性：

　　我们像之前一样可以把 softmax 分解成和：