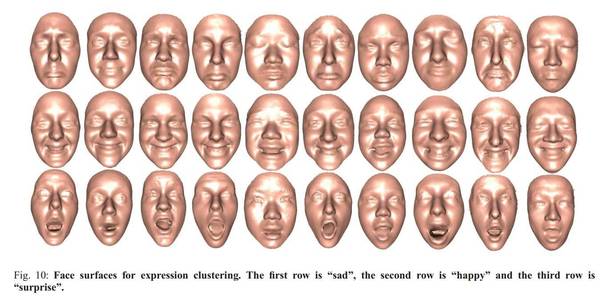
新智元启动 2017 最新一轮大招聘：。

　　新智元为COO和执行总编提供最高超百万的年薪激励；为骨干员工提供最完整的培训体系、高于业界平均水平的工资和奖金。加盟新智元，与人工智能业界领袖携手改变世界。

　　简历投递：j[email protected] HR 微信：13552313024

　　【新智元导读】2017年5月7日，中国人工智能先驱、著名数学家吴文俊先生仙逝，令人无限感伤。顾险峰教授在本文中回顾了吴文俊先生的思想对其学术研究的影响。其中包括对“计算机视觉-吴方法”“人工智能-机器定理证明”等方面的介绍。

　　【顾险峰】：今天（2017年5月7日）惊闻吴文俊先生仙逝，宛若晴天霹雳，令人无限感伤。我虽然从未有幸和吴先生见面，但却多次通过电子邮件得到他亲自教诲。我的学术生涯受到了吴文俊先生光辉思想的深刻影响。

　　中国风格的数学-构造性算法

　　在我学习数学的历程中，所接触的主要定理和理论框架都是由西方人所创立，极少见到中国数学家的名字。更有极少数西方学者狂妄宣称：中华民族虽然历史悠久、人口众多，但是只积累了经验性的知识，对于人类文明没有实质性贡献。年轻时代，我在北美留学，西方同学的轻蔑经常令我悲愤而无奈。直到学习了吴先生关于中国古代数学的系统论述，才令我体会到中国传统数学的伟大和深邃。

　　西方主要遵循公理体系，依靠逻辑演绎来构建数学大厦；吴先生指出中国古代的数学传统是依靠算法来构造理论体系。为了真正将抽象晦涩的纯粹数学转化成切实的生产力，只有逻辑演绎是远远不够的，必须建立构造性证明。在绝大多数的情况下，构造性证明方法的难度远超过逻辑演绎的方法。

　　比如，如下图所示的三维人脸表情分类问题：给定带有表情的三维人脸曲面，如何自动将其依照表情分类。一种方法是将人脸曲面保角地映到平面单位圆盘，将曲面的面元定义为圆盘上的概率测度。不同概率测度间可以计算最优传输映射，传输映射的代价给出了概率测度间的Wasserstein距离。通过Wasserstein距离，我们可以将曲面进行分类。这里最优传输映射等价于求解蒙日-安培方程，其解的存在性证明由Alexandrov用代数拓扑方法给出。这种方法无助于直接求解。数十年后，在丘成桐先生的指导下，我们发现了基于变分法的构造性方法，从而真正实现了几何数据分类的实用算法。

　　从历史观点来看，现代计算机科学的迅猛发展，要求将纯粹数学的抽象理论进一步发展成构造性算法，从而利用计算机来改造社会和自然，而这正是中国数学源远流长的传统。数十年来，我的科研工作集中于计算共形几何，本质上就是将纯粹数学中的共形几何改造成完全基于构造性证明的算法体系，从而彻底与计算机科学融合。其过程异常曲折和艰辛，既有学术研究方面的本质难度，又有社会因素。

　　图1. 曲面单值化定理。

　　从学术方面而言，同一个几何理论有多种理解方式和证明途径，但是真正能够发展出成熟算法的途径往往需要对各种相关理论全都透彻理解并且深入尝试之后才能找出。例如图1所示的曲面单值化定理，任何封闭带黎曼度量的曲面，都可以找到一个新的度量，和初始度量共形等价，同时高斯曲率为常值。为了寻找这一基本定理的构造性证明，我们十数年如一日，尝试了很多方法，经历了许多挫折，包括基于非线性热流方法的调和映照，基于Hodge理论的全纯微分和曲面里奇流方法等等。从社会因素而言，传统的纯粹数学家认为基本几何定理已经发掘，构造性证明原创性不大，因而予以忽视；传统的计算机科学家认为如此抽象的学院派理论和实际相距太远，或者经验性的方法虽然不够严密，但是足够实用，因此难以支持。在过去的岁月中，我们经受了很多挫折和磨砺，每当事业遇到低谷，沮丧犹疑之际，我们就会重温吴先生的工作。吴先生关于中国数学传统的深刻洞察，吴先生关于构造性证明的价值观念，特别是吴先生特立独行，坚持自己的数学品味，无一不给我们巨大的精神支持和鼓励。