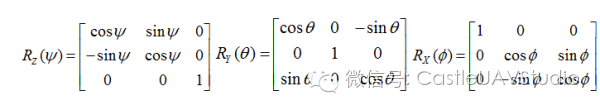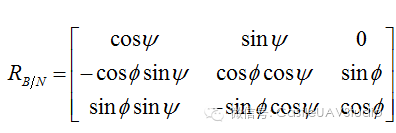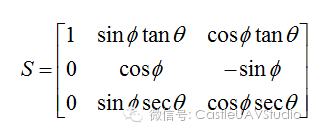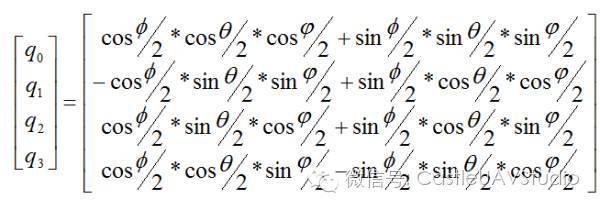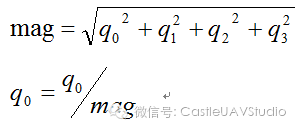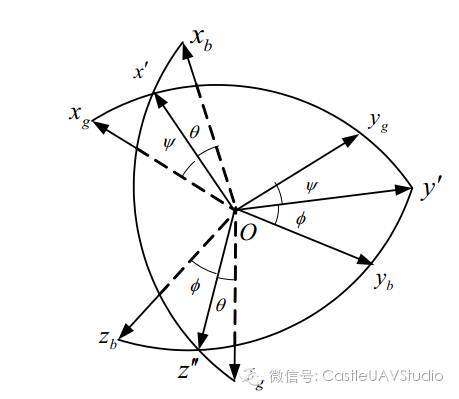
有多种方法对无人机旋转运动进行描述，最常见的是方向余弦和四元数及指数表现形式。但无论是哪一种，我们都可以理解为是按照某种表现方式提供一组基向量，来描述无人机位置的三个自由度。但是它们却因为算法的不同，具有不同性质，这些性质将决定我们对它们的选择。

　　1)欧拉角

　　无人机围绕机体系三轴的运动可以分解为：绕Xb轴的横滚运动，绕Yb轴的俯仰运动以及绕Zb轴的偏航运动。欧拉角直观地将无人机旋转姿态转化为机体坐标系和NED坐标系之间的夹角关系。

　　一说到角度，一定是同一个平面内线和线的关系或者相交平面之间的关系。在无人机坐标系中需要大家建立起六个面的抽象图形，机体坐标系下三个平面：

　　以及NED坐标系下三平面：

　　当我们确立了这六个平面之后，就可以描述无人机姿态了。我们定义横滚角,俯仰角,偏航角来分别描述无人机的横滚运动，俯仰运动，偏航运动。

　　2)方向余弦

　　实现从NED坐标系到机体坐标系的数据变换有什么意义呢？无人机的旋转运动相对于无人机自身是没有任何意义的，因为它相对于自己永远是没有运动的，只有相对于地面（参考坐标系）才有意义。因此我们要用NED和机体坐标系间的关系来表述无人机旋转运动，无疑，矩阵就是描述旋转最好的工具了。

　　我们可以把无人机任意一次旋转按次序拆分为三个部分：绕轴的偏航运动、绕轴的俯仰运动、绕轴的横滚运动。每一次运动用一个旋转矩阵来描述就成为了下面的形式：

　　大家一定注意到这三个矩阵都是斜对称阵，喜欢矩阵的朋友可以自行思考一下，肯定可以挖掘出很多有趣的内容。容易得到从NED到机体坐标系的坐标变换矩阵（方向余弦矩阵）：

　　从机体坐标系到NED坐标系的方向余弦矩阵很容得到：

　　如此一来，我们就很容易实现两个坐标系下信息的相互转换。

　　3)不唯一与奇异性

　　在任何系统中，控制工程师首先关注的是系统方程解的唯一性和存在性。

　　欧拉角非常直观，但也存在两个问题：1.不唯一2.奇异性。这两者分别对应了解的唯一性和存在性。这两个问题从直观上比较难以描述，但从数学上借助方向余弦可以很清楚的解释。

　　不唯一性：举一个例子，令

　　这时：

　　很容易看出，这种不唯一性是由三角函数的周期性引起的，不唯一性可能会出现系统运动不按照我们期望的方式进行。

　　奇异性（局部）：如果我们令：

　　这会带来什么问题呢？在后面介绍无人机数学模型时，三个欧拉角与无人机本身的旋转角速度是通过一个矩阵进行关联的：

　　此时，零出现在分母上，这时控制器就没有办法处理被控对象的数学模型了，也就是我们所说的解不存在的情况，也将因此无法实现有效控制。这就是常说的“万向节锁死”。数学描述是不是非常直观明了呢？

　　上面的情况导致欧拉角的姿态描述方式在某些姿态情况下不可使用，这对于无人机控制而言是会带来一定风险的。因此我们需要在另外一种描述方法可以对无人机所有的姿态进行描述。

　　4)四元数

　　四元数是一种全局的姿态描述方法，换句话说，当使用四元数描述姿态的时候，纵使

　　再次出现，描述方法依然有解。我们 直接验证一下就可以了，首先看一看如何从欧拉角获取四元数：

　　然后再对四元数进行归一化处理：

　　q1,q2,q3的归一化处理与q0相同。