根据演化算法的工作原理，该方法将经过训练的架构视为个体。因此，我们能够创建具有多个模型的群体，并将适应度值视为验证集的精确度。本文建议使用图形作为数据结构来编码个体的基本架构。在这个设计图中，顶点表示 3 级张量，这在卷积神经网络中十分常见：使两个维度作为图像的空间坐标，而第三个张量表示 RGB 颜色通道；图形的边缘则表示连接、卷积或可变参数。随后我们通过删除低适应度值模型来应用进化规则，并选择最优的父代来产生新的个体。在繁殖过程中，为了增加个体多样性，我们也会使所选父代的复制版产生突变，接着会在大型搜索空间中重复进行随机个体的成对比赛，以寻得最终的最优子代。对于具体的规模实现，atv，我们已经开发了大规模并行的无锁基础设施。不同的计算机将进行异步操作，并在表示个体的文件目录之下，依靠共享文件系统进行通信，atv，移除和垃圾回收也将被用于处理计算效率问题。此外，繁殖过程对整个群体进行了演变。变异操作也会从预定集中随机选择。变异操作包括：

更改学习率（下文会列出抽样细节）。

身份（实际是指「保持训练」）。

重设权重（如 He et al.（2015）的样本）。

插入卷积（在「卷积主干」中的随机位置插入卷积，如图 1 所示。插入的卷积具有 3×3 的滤波器，随机步长为 1 或 2，信道数量与输入相同。可以应用批量归一化及 ReLU 激活，也可不进行随机使用）。

消除卷积

改变步长（仅允许幂为 2 的步长）

改变任一卷积的信道数。

过滤器尺寸（水平或垂直方向随机，并随机选择卷积，但仅为奇数值）

插入一对一（插入一对一或身份连接，类似于插入卷积突变）

添加跳过（随机层之间的身份）

删除跳过（删除随机跳过）

在突变过程中，所有参数都会产生一个密集的搜索空间，这意味着任何参数都不存在上限。因此所有的模型深度都能够实现。参数的这种无限性引起了对可能存在的真正大型架构集的探索。换言之，神经网络的参数与架构都能够在没有人为干预的条件下演化。

经过对理论背景的阐释，我们逐步介绍了将要做的实验的初始设置与验证策略。众所周知，在初始化方面，即便是一个经过训练的卷积神经网络也属于强分类器，它还可能在实验中达到相对较高的精确度，因此本文会从简单个体所组成的群体出发。这些个体不包含卷积以及在分类方面性能不佳的网络，同时其学习率会被初始化为很大的值：0.1。这种设置会强制个体进行学习，使强分类器进行演变，并能通过变异进行自我发现；同时实验可以避免「操控」，进而大获成功。

加速演化的另一种策略便是权重继承。此处的继承是指，只要有可能，个体便可继承父代的部分或全部权重。在报告方法中，每次指的都是「最佳模式」。除了在一个实验中选择最佳模型，具有最高验证精确度的模型还试图在所有实验中选择「最佳实验」。

除了训练和测试策略，计算成本是实验的另一个重要方面。它由 TensorFlow 实现，其中基因变异和卷积可被视为 TF（TensorFlow）操作。对于每一个 TF 操作，我们都会预测所需浮点运算（FLOP）的理论数，并在给定每个个体后分配计算成本：

其中 F 表示用于训练和验证的 FLOP，E 表示正在运行的时期，N 表示训练和验证的样本数量。此外，每个实验的计算成本是其全部个体成本之和。

下一步是去实现上文提到的算法。每个实验需要在几天内演变出一个群体，如下图所示：

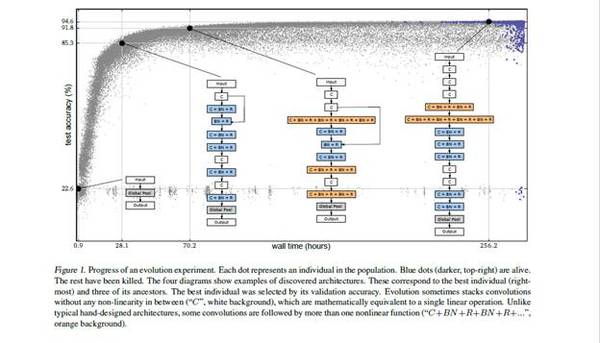
图 1. 演化实验进展。每个点代表群体中的个体。蓝点（黑色，右上）表示存活个体，其余个体已被杀死。四个图表展示了发现的例子。这些对应于最优的个体（最右）以及它们的三个祖先。最优个体通过其验证精确度进行选择。演化有时会在不存在任何非线性的区域（「C」，白色背景）之间堆叠卷积，这在数学上与单个线性运算相同。一些卷积则与典型的人工设计架构不同，其后伴随着多个非线性函数（「C + BN + R + BN + R + ...」，橙色背景）。