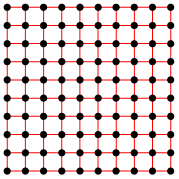
无论是量子物理还是复杂网络，我们都能从中看到由关系、标度、自相似、双曲几何相互交织的大网。也许这是一种能够统领宏观与微观的统一理论，这是一种面向关系的物理学。

　　撰文

　　张江（北京师范大学系统科学学院副教授、集智俱乐部创始人）

　　城市中的社交网络

　　我们的社交圈子就是一张无穷无尽的大网，而每个人就像落入的飞虫，无法看到整张网络的全貌。

　　真实的社交网络是什么样子的？起初人们猜想，那应该很像一个规则的网格，如图1所示。

图1. 规则网络，每个节点都只与它的欧氏距离最近的节点相连

　　这种思考不无道理，由于我们的城市就好像一张规则的几何平面，而每个人都生活在几乎等大小的格点之中（如图2所示），于是如果人和人之间的社交关系都仅仅限于邻里之间的话，那么规则网格就成为了必然结果。

　　图2. 规则的城市，每个人都生活在规则的格子中

　　然而，我们很容易知道真实情况一定不是这样子的。原因是，没有哪个人愿意成天宅在家里，于是人们发明了城市道路来沟通，这样真实的城市除了一些规则的社区之外，还存在着类似于血管网络一样的街道，如图3所示。

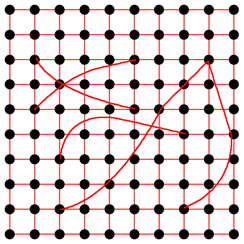
图3. 巴黎城市上空的夜光图

　　这些血管不仅将城市支离破碎成一个个不规则的小区域，而且还成为了沟通两个不同小区之间的超级“虫洞”（或称传送门 Portal）——这是因为，人们可以通过现代化的交通工具快速地到达城市的远方。于是，我们猜测，社交网络也会随着“虫洞”的出现而变形：我们有大量的邻居朋友们，但同时还保持着一些遥远世界的朋友，这样网络中会出现一些长程链接（如图4所示）。

　　图4. 猜测的社交网络

　　这种长程联系可以使得网络的平均距离大大缩短，于是我们通过将近六步跳跃就可以通达整个网络，这就是所谓的六度分离现象。而作为背景的网格则使得社交关系具有高度的集聚性，也就是说你的朋友们彼此相连的概率依然很大。科学家们将这类平均距离很短、集聚性很高的网络称为小世界网络。

　　大量紧密相连的局部链接配上少数长程的“虫洞”使得整个网络处于一种牵一发而动全身的临界状态。物理上，这些处于临界态的系统通常具有标度对称性。

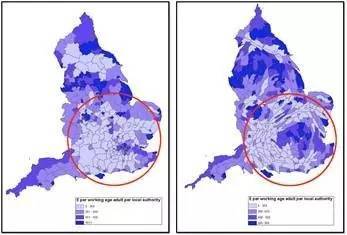
　　图5. 互联网：节点为路由器，连线为物理链接

　　如图所示，当我们用放大镜去看这个复杂网络的时候，会发现它仿佛是一座大型的分形城市，有中心，有社区，也有小镇和村庄。当我们把放大镜的比例不断提升，就会发现大大小小的团簇跃然纸上，更重要的是，它们都是彼此相似的。在定量上，这种自相似性就体现为一系列的幂律关系和幂律分布，著名的网络科学家巴拉巴希（Albert Barabasi）将这种处于临界态的网络称为无标度网络。

　　复杂网络的双曲几何

　　那么，我们是否可能设计一个模型来复现出同时具备小世界和无标度特性的网络呢？

　　让我们仍然从城市的类比中寻找灵感。我们都知道，城市无非就是大量人口的聚集。然而，这些人口并不均匀地分布在城市区域之中，而通常会形成中心密集、外围稀疏的分布形态。假如我们硬要将城市的形态绘制成等密度分布，那么城市就会发生一定的扭曲变形：中心区域会膨胀得很大，而外围区域则会被挤压变得很小。这在地理学中就叫做等人口密度图（Cartogram map），如图6所示。

　　图6. 伦敦原图（左）与它的等密度图（右），图中红色圆圈圈起来的区域就是大伦敦区，它基本上是一个对称的圆形区域，并呈现了中心人口密集，外围稀疏的特性。将大伦敦区的等人口密度图展现出来就仿佛是一个双曲空间的庞加莱圆盘模型。