1. 状态值函数（State-value function）：指在 S 状态和π策略下获得的预期返回值，这个返回值的计算方法是：将每一次移动的奖励相加求得出的值（γ 指常数折现系数，意思是第10 次移动获得的奖励要比第1 次移动获得的奖励小一些）。

　　2.行为值函数：在S状态和π策略下进行一个操作的预期奖励值（等式同上，除非有另外的情况At = a）。

　　解开 MDP 式子

　　下面就来解这个MDP式子，可以解出任何状态下程序奖励的最大值，也就是最佳行为（策略）。利用动态程序设计，确切地说是策略迭代法，可以解出一个最优策略。（其实还有另外一个方法——数值迭代法，atv，这里就不多赘述了）。思路是使用一些原始策略 π1，求出状态值函数的值。利用 Bellman 期望方程（Bellman expectation equation）来解。

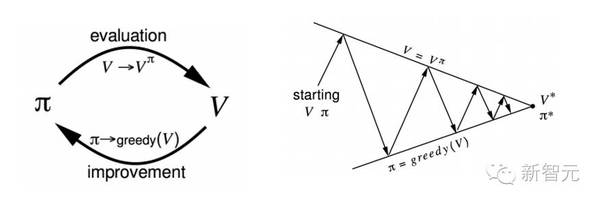
　　方程的意思是，在 π 策略下，可以解出的中间奖励 Rt+1 预期奖励总和以及接续状态 St+1的值函数。注意看的话可以发现，这跟上一段的值函数定义是一样的。使用这个方程式是策略计算的一部分。为了得到更好的策略，我们采用一个策略提高步骤，根据值函数进行操作。换句话说，程序会执行返回最大值的操作。

　　为了获得最优策略，我们重复以上两个步骤，反反复复，直到得到最优策略π*时系统停止操作。

　　没有给定 MDP 怎么办？

　　策略迭代法虽然很强大，但是只有给定了 MDP 才可以操作。MDP 会给出环境是如何操作的，但这在现实情况下是做不到的。没有给定MDP时，可以采用无模型法，直接进行程序和环境的体验或交互，得出值函数和策略。没有给定MDP信息时，j2直播，直接进行策略计算和策略提高的重复操作。

　　这种方法下，我们不用过度优化状态值函数的方法来提高策略，而是通过过度优化行为值函数来实现。下面是将状态值函数分解成中间奖励总值和接续状态值函数的方法。

　　下面 jieshao 重复过程策略计算和策略提高的过程，除非行为状态值Q代替了状态值函数V，具体的过程细节这里不细讲。要理解 MDP 的 free evaluation 和提高方法，就得要把 Monte Carlo 学习算法、时序查分算法、SARSA 学习算法的相关博文全部看一遍。

　　值函数逼近

　　学到这一步，下面我们将用相对简单的方法来说。根据上面的 Q 等式，给定状态 S 和行为A，可以计算出一个数，接近于预期奖励。可以想象一下，程序每向右移动 1 毫米，都可以得出一个新的状态 S，进而计算出一个 Q 值。

　　但是，在现实的强化问题中，有数百万种状态，所以值函数的概括功能就显得尤为重要，这样就不需要计算每一个状态下的值函数。解决方案是用Q值函数逼近大方法概括出未知的状态。利用Qhat函数计算出Q值在特定状态S和特定行为A下大概的近似值。

　　在这个函数中代入S、A和权向量W（采用梯度下降算法），计算出x（代表S和A的特征向量）和W之间的点积。要提高函数精确度，就要计算出真实Q值与输出的近似函数之间的差。

　　计算出差值后，采用梯度下降算法求出最小值，进而得出最优的W矢量值。这种函数逼近概念在下面的论文中会有重点讲述。

　　强化学习中的探索与开发

　　最后一点非常有意思，值得讨论，即强化学习中的探索（exploration）与开发（exploitation）。

　　开发是指程序执行已知的过程，并作出奖励最大化的操作。程序总是会根据它已有的知识体系去执行最优的操作，这里强调它拥有一个已有的知识体系。但是如果程序并不熟悉所有的状态空间，那么可能就无法做出最优的操作，这种探索状态空间的操作就叫探索。